Linear Algebra – Farm inventory.
In this example we will use the functionality of the use of determinants in linear algebra to solve an inventory problem on an agricultural farm.
The scenario is to know how many pigs and how many chickens the farm currently has, based on a system of linear equations.
.
Definition of variables in the problem.
First we will define the variables that represent the current problem, as follows it is simple to adapt and we will choose the variables X for the number of pigs and Y for the number of chickens to count.
The problem is based on the fact that we only have the following data to consider.
1.- The total number of heads between pigs and chickens is 35.
2.- The total number of legs between pigs and chickens is 110.
With the above data we must calculate how many animals there are of each, both pigs and chickens individually.
.
Algebraic representation of the problem.
To create the system of linear equations that represent the problem we must consider that pigs have 1 head and 4 legs, just as chickens have 1 head and 2 legs, this gives us the following system of equations below.

We must consider that the sum of the heads of X pigs and Y chickens gives us a total of 35, on the other hand, the total sum of the legs is 110, considering that pigs have 4 legs and chickens have 2 legs, it would be represented as 4X for pigs and 2Y for chickens.
Once we have the system of equations, we proceed to solve it using determinants in the following way.
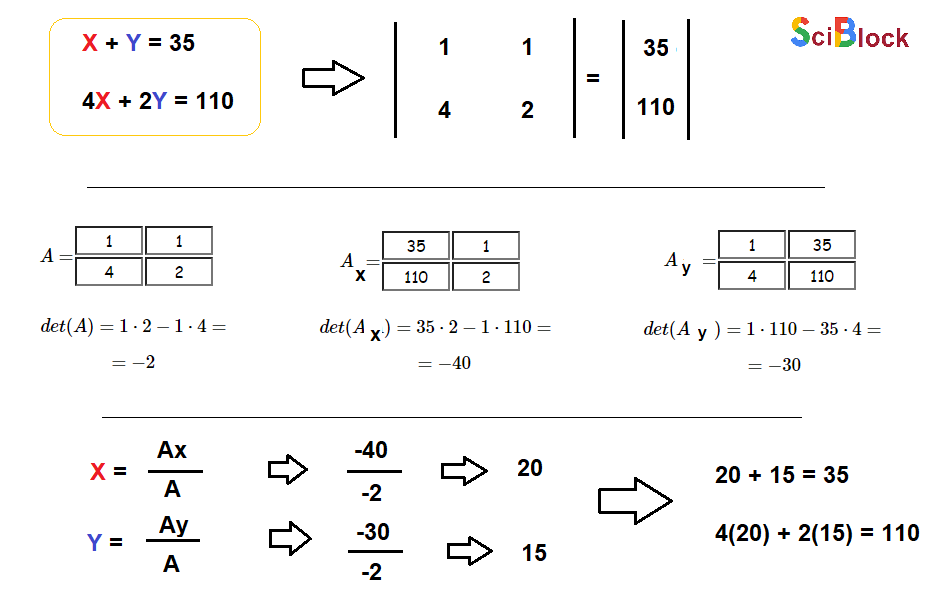
Applying the use of extension with determiners.
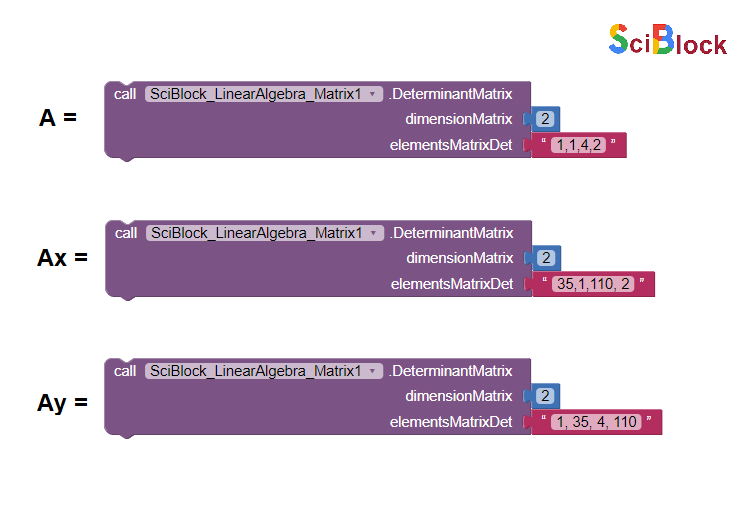
Solution (Result):
As we can see, the final result is: 20 pigs and 15 chickens.
.
Generic example of use.
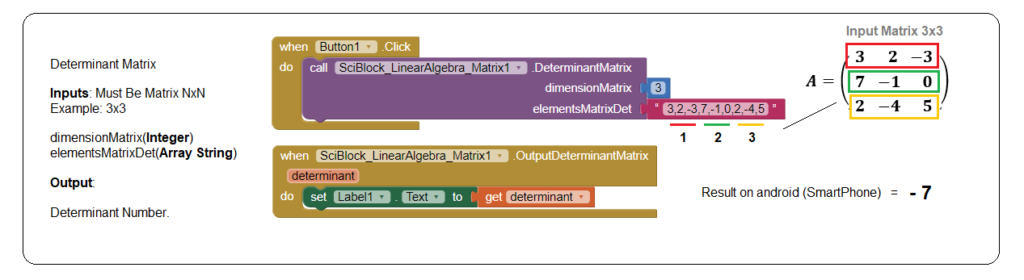
.